[ComputerScience bootcamp with python 2장]

in Python on BootcampPython


본 포스팅은 컴퓨터사이언스 부트캠프 with 파이썬 이라는 책을 참고하여 개인 공부를 하면서 정리하고 있습니다.

문제 될 시 삭제하겠습니다.

Chapter 2 정수

수(number)는 컴퓨터가 다루는 데이터 종류(자료형) 중 가장 중요

2-1. 컴퓨터에서 수를 표현하는 방법

  • 수를 표현하는 방법을 기수법(numeral system)이라고 함

    기수법이란? 수를 시각적으로 나타내는 방법

    • 10진수는 0~9의 10개의 숫자를 수로 표현 (사람의 방식)
    • 2진수는 0과 1의 2개의 숫자로 수를 표현 (컴퓨터의 방식)
    • 16진수는 0~9, A~F의 10개의 숫자와 6개의 알파벳으로 수를 표현

2-1-1. 10진수

  • 10진수 수를 표현하는 데 숫자 총 10개 사용
  • 밑수는 10, 0부터 9까지 총 10의 숫자
0, 1, 2, 3, 4, 5, 6, 7, 8, 9

2-1-2. 2진수

  • 숫자 0과 1만 사용
  • 컴퓨터가 인식할 수 있는 표현 방법
0, 1

2-1-3. 16진수

  • 16진수는 수를 표현하는 데 총 16개 사용
  • 9 이후의 숫자는 알파벳 a ~ f 표현

16진수 표현

2-2. 10진수를 2진수로

  • 10진수 25를 2진수로 바꾸려면?

    1. 25를 2의 거듭제곱의 합으로 쪼갬

       25 -> 16 + 9

    2. 9에 가장 접근한 2의 거듭제곱 수는 8(2^3)

       25 -> 16 + 8 + 1 = 2^4 + 2^3 + 2^0

    3. 2^2이나 2^1처럼 중간에 빠진 지수는 0을 이용하여 표현

       25 -> 1x2^4 + 1x2^3 + 0x2^2 + 0x2^1 + 1x2^0

    4. 2의 거듭제곱 수를 제외하고 앞의 수 1과 0만 모아 나열

       1x2^4 + 1x2^3 + 0x2^2 + 0x2^1 + 1x2^0 => 11001

    25를 2진수로 변환하면 11001

    파이썬 코드를 이용해 25가 2진수로 바르게 변환하는지 확인

      bin(25)
  '0b11001'

    bin() 함수는 2진수로 표현하는 함수

    결과 값 앞에 나오는 0b는 2진수를 의미

2-3. 2진수를 10진수로

  • 반대로 2진수를 10진수로 바꾸면?

    1. 그림 같이 11001 위에 오른쪽 끝부터 0, 1, 2, 3, 4 를 차례로 적는다

      2진수를 10진수로?

    2. 위에 적어 둔 수를 지수로 활용 2의 거듭제곱 수의 합으로 표현

       1x2^4 + 1x2^3 + 0x2^2 + 0x2^1 + 1x2^0

 16 + 8 + 0 + 0 + 1 = 25

2-4. 16진수를 2진수로

  • 2진수와 16진수 사이의 진수 변환

    16진수

  • 마지막 15를 2진수로 변환하면 1111
    • 16진수 한 자리는 2진수 네 자릿수까지 표현가능
      f = 1111
  • 16진수를 2진수로 변환할 때 0부터 9까지 변환하는 방법 = 10진수 2진수 변환

    • 16진수 9를 2진수로 변환한다면?

      1. 9 -> 8 + 1 = 2^3 + 2^0
      2. 2^3 + 2^0 = 1x2^3 + 0x2^2 + 0x2^1 + 1x2^0
      3. 결과값 = 0b1001

  • 그럼 a는 어떻게 변환될까? 참고로 a는 10진수로 10

    1. 10 => 8 + 2 = 2^3 + 2^1
    2. 2^3 + 2^1 = 1x2^3 + 0x2^2 + 1x2^1 + 0x2^0
    3. 결과값 = 0b1010
  • 16진수 b부터 f까지를 2진수로 모두 변환하면?
    • b는 10진수로 11 => 0b1011
    • c는 10진수로 12 => 0b1100
    • d는 10진수로 13 => 0b1101
    • e는 10진수로 14 => 0b1110
    • f는 10진수로 15 => 0b1111
  • 8비트 컴퓨터의 메모리 주소가 2진수로 0010 1101
  • 2진수 네 자릿수를 16진수 한 자릿수로 표현가능 => 0x2d
address_8bit = 0b00101101
hex(address_8bit)
>>> 0x2d

hex()함수는 정수를 16진수로 표현

2진수로 표현하면 8비트를 표현하는데 여덟 자릿수가 필요

16진수로 표현하면 두 자릿수로 간단히 표현할 수 있으며 가독성도 높일 수 있음

이러한 이유로 메모리주소를 나타낼 때는 16진수를 사용

  • 32비트 컴퓨터는 서른두 자릿수의 2진수 수가 아닌 여덟 자릿수의 16진수 수를 이용해 표현
address_32비트 = 0x1234abcd
bin(address_32비트)

>>> 0b10010001101001010101111001101

2-5. 양의 정수

  • 컴퓨터는 정수를 1바이트, 2바이트, 4바이트, 8바이트 등 다양한 크기로 저장
  • 정수에는 양수와 음수가 있으므로 부호를 나타내는 데 1비트를 사용
    • 맨 앞의 비트가 0이면 양수, 1이면 음수
  • 25를 메모리에 저장할 때 맨 앞의 비트는 양수이므로 0

  • 10진수 25를 2진수로 변환하면 11001 => 나머지 비트를 0으로 채우면?

    8비트 형태

    맨 앞의 비트가 부호를 나타냄

1바이트로 나타낼 수 있는 수의 크기는?

언뜻 생각하면 8비트를 사용하니까 2^8 즉, 0~255일 것 같지만,

정수에는 음수가 포함되며 맨 앞의 비트를 부호로 사용하므로

표현할 수 있는 양수의 범위는 절반으로 줄어듬

즉, 1바이트로 나타낼 수 있는 수의 범위는 -128 ~ 127

(음수를 취급하지 않아 0 ~ 255로 나타낼 수 있는 정수 자료형도 있음)

2-6. 음의 정수

음의 정수가 어떻게 저장되는지 이해하려면 보수의 개념을 알고 있어야 한다

2-6-1. 보수의 개념

  • 보수란 쉽게 말해 ‘보충해 주는 수’
  • 예를 들어 10진수에서 9의 보수를 구한다고 가정
    • 3의 9의 보수는 3을 더해 9가 되는 수인 6
    • 26의 9의 보수는 73

어떤 수의 각 자릿수 수를 9에서 빼면 9의 보수를 구할 수 있다

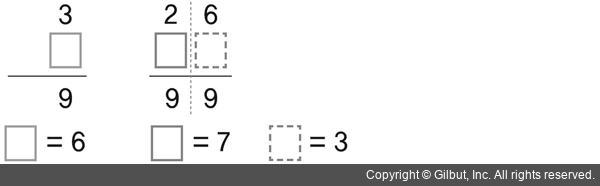
16진수 표현

  • 10의 보수도 구해보자
    1. 3의 10의 보수는 3의 9의 보수인 6에 1을 더한 값인 7
    2. 26의 10의 보수는 9의 보수인 73에 1을 더한 값인 74

  • 123의 9의 보수와 10의 보수를 구하면?

    16진수 표현

    한 자릿수 수나 두 자릿수 수와 같은 원리

2-6-2. 2의 보수

  • 2진수 1010의 1의 보수는?

    • 10진수에서 9의 보수를 구할 때 9에서 각 자릿수 수를 뺏으니, 1에서 각 자릿수 수를 빼면 됨

      0101

      • 각 자릿수 수의 1과 0을 반전한 결과

    • 이제 1010의 2의 보수를 구하면?

      1010의 1의 보수가 0101이므로 여기에 1을 더하면 됨

      즉, 1010의 2의 보수는 0110

2의 보수가 중요한 이유는 컴퓨터가 음수를 표현할 때 2의 보수를 사용하기 때문

2-6-3. 음수의 표현

컴퓨터는 음수를 2의 보수로 표현

  • 음수인 -4는 어떻게 표현??

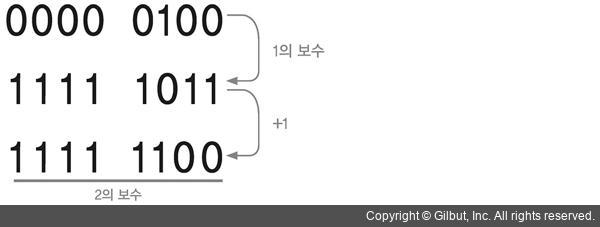
    16진수 표현

    1. 4를 2진수 (0000 0100)로 변환하고 1의 보수를 구함
    2. 1에서 각 자릿수 수를 빼면(모든 비트를 반전) 1의 보수인 1111 1011
    3. 이 수에 1을 더해 2의 보수를 구하면 최종 결과는 1111 1100

    즉, 컴퓨터는 -4를 1111 1100으로 표현

      (-4).to_bytes(1, byteorder='little', signed = True)

  >>> b'\xfc'

    이 코드는 -4라는 정수를 컴퓨터 메모리에 저장되는 바이트형태로 표현하는 코드

    • 첫번째 인자는 몇 바이트로 나타낼지 지정 (지금까지 예를 1바이트로 진행했으므로 1로 지정)
    • 두번째 인자는 바이트 오더(byteorder)
    • 마지막 인자인 signed는 양수와 음수를 모두 표현할지 아니면 양수만 표현할지 정하는 인수

    출력 값은 16진수로 표현

    16진수 0xfc를 2진수로 변환하면 1111 1100

    이로써 컴퓨터는 음수를 2의 보수를 이용해 저장한다는 걸 알 수 있다

2-6-4. 2의 보수로 표현하는 이유

컴퓨터는 왜 음수를 2의 보수로 저장할까?

  1. 양수와 음수를 모두 양수처럼 저장한다고 가정

    0000 0000과 1000 0000은 +0과 -0

    즉, 0을 표현하는 두 가지 방법이 존재

    이렇게 되면 컴퓨터 입장에서는 수 하나를 더 표현할 수 있는데 비트 하나를 낭비하는 셈

    또한, 두 수를 비교할 때 CPU에서 뺄셈을 하는데 +0과 -0을 비교하면 결과 값이 다르게 나옴

  2. 컴퓨터에서 정수의 뺄셈 과정을 살펴보자

    • 덧셈은 단순히 두 수를 더하면 되지만, 뺄셈은 2의 보수 개념을 활용

      정수의 뺄셈 연산

      10진수 9를 2진수로 표현한 0000 1001에서 10진수 -4를 2의 보수로 표현한 1111 1100을 더함

      계산 결과를 보면 받아올림이 발생하여 1 0000 0101이 나옴

      이때 맨 앞 네모 안에 있는 1 버림

      최종 결과는 0000 0101 로 5가 됨




© 2018. by Dev_Yonghee

Powered by Dev_Yong